
Публикации
- Главная /
- Публикации /
- Моделирование режима зарядки литий-железо-фосфатной аккумуляторной батареи с учетом разброса параметров отдельных аккумуляторов
Моделирование режима зарядки литий-железо-фосфатной аккумуляторной батареи с учетом разброса параметров отдельных аккумуляторов
А.Н. Ворошилов – главный инженер ООО «Системы накопления энергии».
Е.А. Чудинов – профессор, д.т.н, руководитель проектов ПАО НЗХК.
А.Н. Петров – руководитель проектов ПАО НЗХК.
Статья опубликована в информационно-справочном издании "Новости электротехники" 2017 – №2 с. 44 – 49
Ключевые слова
Литий-железо-фосфатная аккумуляторная батарея, математическая модель батареи, режим зарядки, влияние разброса параметров.
Введение
Литий ионные аккумуляторы (далее - ЛИА) – сравнительно новая технология накопления электрической энергии, которая быстро развивается в последнее время. По своим параметрам (плотность запасаемой энергии, плотность мощности, ресурс при циклировании) данный тип химических источников тока значительно превосходит традиционные (свинцово-кислотные и щелочные) аккумуляторы. В связи с постоянным улучшением технологии производства ЛИА, наблюдается последовательное снижение стоимости данного типа аккумуляторов. Сегодня стоимость запасаемой в них энергии лишь незначительно превышает стоимость энергии, запасаемой в традиционных аккумуляторах. Это обеспечивает экономическую целесообразность их использования во все более широких областях техники.
Из всех известных типов ЛИА с использованием в качестве материала катода литий-железо-фосфат (LFP) является по настоящему безопасным в эксплуатации, а допирование активной массы катода некоторыми металлами существенно улучшает энергетические характеристики этих аккумуляторов. Эти факты обусловили большой интерес, проявляемый к ним производителями накопителей энергии для электротранспорта и энергетики. Вместе с тем данный тип литий-ионных аккумуляторов, по сравнению с другими типами ЛИА, имеет ряд особенностей, учет которых необходим для обеспечения требуемого ресурса их эксплуатации. В статье рассматриваются особенности эксплуатации ЛИА LFP, а также приводятся некоторые результаты математического моделирования процесса зарядки литий-ионной аккумуляторной батареи (далее – ЛИАБ), собранной на их основе, с учетом разброса параметров отдельных аккумуляторов. При этом сам аккумулятор рассматривается как активный двухполюсник, параметры которого (напряжение генератора и внутреннее сопротивление) нелинейно зависят от тока зарядки/разряда, степени заряда и температуры. При моделировании использовался массив экспериментальных данных, полученный на заводе Лиотех в течение 2014-2015 гг. Результаты исследования могут быть использованы для повышения эффективности зарядки ЛИА LFP и обеспечения длительного ресурса их эксплуатации.
1. Режим зарядки ЛИА LFP
1.1. Вольт-амперные характеристики при зарядке
Характер зависимости напряжения на аккумуляторе при его зарядке или разряде постоянным током имеет специфический характер. На рисунке 1.1 показана типичная зависимость напряжения на ЛИА LFP модели LT-LYP380 производства Лиотех от степени заряда при его зарядке при комнатной температуре (20 + 5ºС).
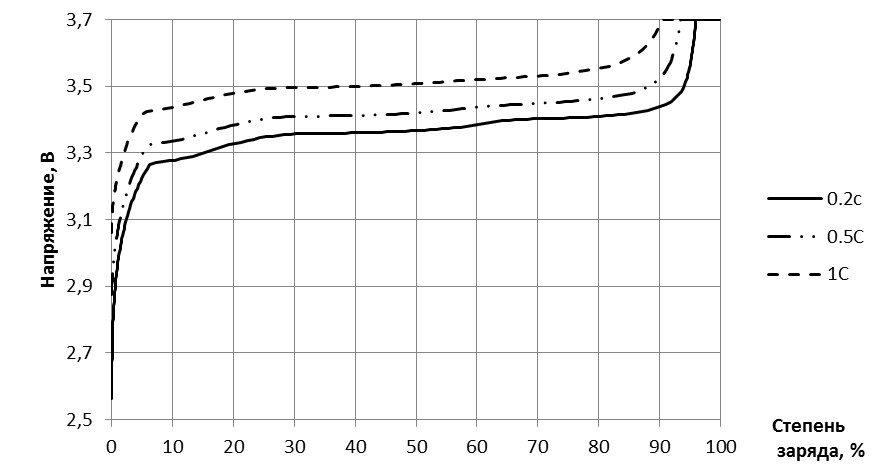

Рисунок 1.1 – Зависимость напряжения на аккумуляторе LT-LYP380AH от степени его
заряда при зарядке разными токами (0,2С; 0,5С; 1С)
Для характеристики зарядки ЛИА LFP характерны три области: быстрой рост напряжения на аккумуляторе в начале зарядки, медленное изменение напряжения в середине и быстрый рост в конце. Большинство производителей ЛИА LFP рекомендуют ограничивать напряжение зарядки аккумулятора на уровне 3,7 – 3,9 В.
1.2 Режим зарядки СС/CV
Наиболее часто применяемым режимом зарядки аккумуляторов является режим зарядки постоянным током (constantcurrent) с переходом в режим постоянным напряжением (constantvoltage), так называемый режим CC/CV. На рисунке 1.2 представлен типичный график зарядки свинцово-кислотного аккумулятора. Красной кривой показана зависимость тока, синей – напряжения от времени. Для литий-ионного аккумулятора характер кривых не меняется, за исключением того, что напряжение перехода в режим зарядки постоянным напряжением для ЛИА существенно выше. Это связано с тем, что напряжение разомкнутой цепи (НРЦ), у ЛИА существенно выше, чем у свинцово-кислотных аккумуляторов. Для ЛИА LFP производители рекомендуют выбирать величину напряжения, равную 3,7 – 3,9 В, для аккумуляторов других типов (NMC, LCo, LTO) эта величина может несколько отличаться.
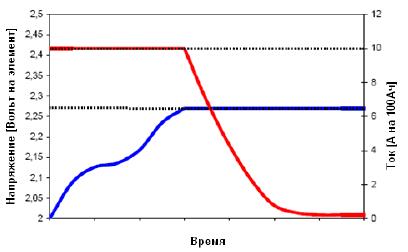

Рисунок 1.2 – типичная зависимость зарядки CC/CV для свинцово-кислотного аккумулятора
При эксплуатации свинцово-кислотной аккумуляторной батареи в режиме поддерживающего заряда, иногда используют режим с двумя уровнями напряжения. При достижении определенной величины степени заряда (S0C) осуществляется переход в так называемый режим поддерживающего заряда. Например, для обслуживаемых свинцово-кислотных аккумуляторов, при комнатной температуре напряжения зарядки равно 2,30 – 2,40 В, напряжение поддерживающего заряда – 2,23 В. Величина напряжения поддерживающего заряда у свинцово-кислотных аккумуляторов выбирается исходя из условия минимизации процессом коррозии его электродов и зависит от температуры эксплуатации свинцово-кислотного аккумулятора. У ЛИА этот переход, как правило, выглядит иначе. В этот момент требуется остановить зарядку вообще, либо снизить ток зарядки до величины тока балансировки. Причины того, что литий-ионные аккумуляторы, входящие в состав батареи, необходимо балансировать между собой будет обсуждаться ниже.
1.3 Режим зарядки стабилизированным напряжением (CV)
Пусть в момент времени t1 от начала зарядки аккумулятора происходит переход из режима зарядки постоянным током в режим зарядки постоянным напряжением. При переходе в режим зарядки постоянным напряжением ток с течением времени падает экспоненциально (см. рисунок 1.3), изменяясь по закону:

.jpg) (1)
(1)
Данная зависимость определяется решением уравнения Коттрелла и Фика для литий-ионных аккумуляторов в режиме потенциостатики. При этом постоянная времени ???? определяется химическим коэффициентом диффузии интеркалирующих частиц, толщиной слоя материала электрода и другими параметрами.
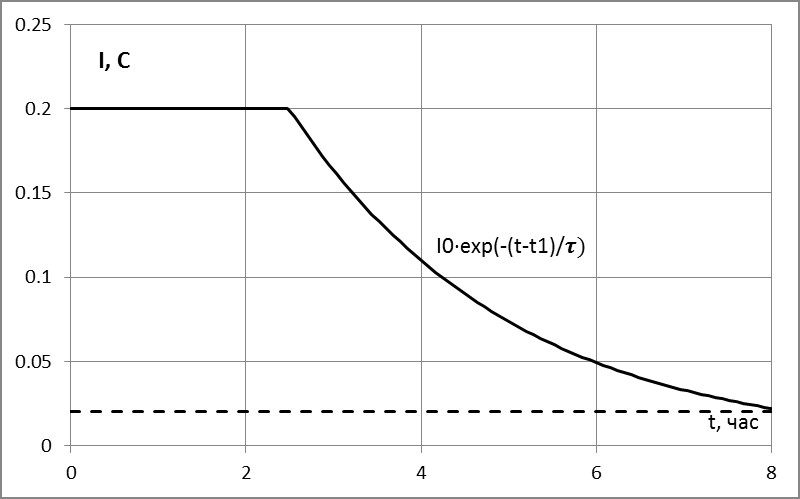

Рисунок – 1.3 – Профиль зарядки аккумулятора в режиме CC/CV
Заряд Q, принимаемый аккумулятором, определяется кулоновским интегралом:

.jpg) (2)
(2)
Решая уравнение (2) и используя выражение (1), можно показать, что:

.jpg) (3)
(3)
Здесь Cн – емкость аккумуляторной батареи.
Для литий-железо-фосфатной аккумуляторной батареи приняты следующие параметры зарядки, приведенные к единичному аккумулятору:
U0 = 3,40 – 3,70 В[1], I0 = 0,2Cн[2], А; t1 ≈ 2,5 – 4,9 час. Время зарядки до снижения тока до уровня 0,1·I0 (этот уровень принят для определения полной емкости аккумуляторной батареи), определяется выражением:

.jpg) (4)
(4)
При U0 = 3,4 В t зар ≈ 8,25 ч, при U0 = 3,7 В t_зар≈5,20 ч. В координатах ток/степень заряда данная зависимость представлена на рисунке 1.4. В реальном случае, когда батарея (или единичный аккумулятор) подключена к зарядному устройству через кабель конечной проводимости, профиль зарядки становится сложнее, так как по мере зарядки батареи снижается зарядный ток, и, соответственно, снижается падение напряжения на подводящих кабелях. Это приводит к увеличению напряжения, приложенного к батарее по мере его зарядки, и профиль зарядки, представленный на рисунках 1.3 и 1.4, искажается.
[1] Значению напряжения 3,40 соответствует переход в режим зарядки VC при степени заряда примерно 50%, 3,70 В – 98%. Это значение может уточняться в зависимости от параметров аккумуляторов разных производителей
[2] Данному значению соответствует ток разряда полностью заряженной батареи в течение пяти часов.
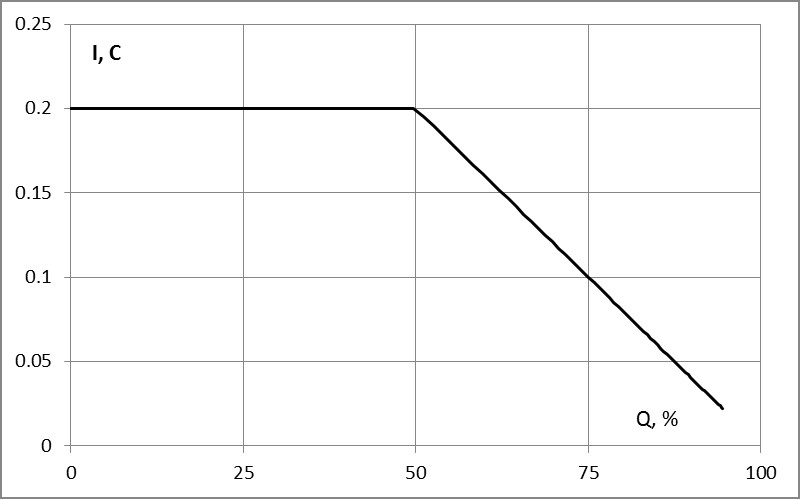

Рисунок 1.4 – Профиль зарядки аккумулятора в режиме CC/CU в координатах ток/степень заряда
2. Параметры LFP аккумулятора
2.1 Эквивалентная схема аккумулятора
На рисунке 2.1а представлена эквивалентная схема активного двухполюсника в общем виде. Здесь E_int – ЭДС генератора, Z_int – его внутреннее сопротивление (импеданс), которое имеет комплексный характер, то есть зависит от частоты. Вообще говоря, E_int и Z_int являются функциями тока, степени заряда, температуры и частоты. Чтобы объяснить характер кривой зарядки ЛИА LFP при приближении степени заряда (State of Charge – SoC) к 100%, необходимо более подробно рассмотреть его эквивалентную схему.
Различные эквивалентные схемы аккумуляторов обсуждаются в ряде работ. Наиболее полный обзор публикаций на эту тему представлен в (1, 2). На рисунке 2.1б представлена эквивалентная схема, которая, на наш взгляд, наиболее адекватно описывает поведение аккумулятора при его зарядке/разряде, измеренное экспериментально.
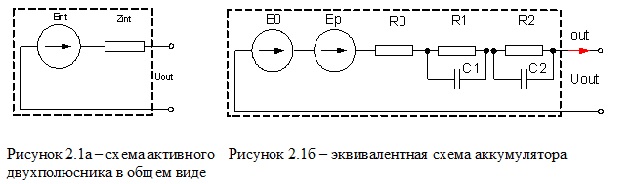

Здесь
E0 - НРЦ - напряжение разомкнутой цепи аккумулятора
Ep - поляризационный потенциал;
R0 - суммарное омическое сопротивление контактов, материала электродов, электролита и т.п.;
C1 - электрическая емкость двойного слоя электрод – электролит;
R1 - сопротивление переносу заряда на границе электрод – электролит;
C2 - электрическая емкость, определяемая градиентом напряженности электрического поля в веществе электролита при протекании через него электрического тока;
R2 - сопротивление, определяемое конечностью значения коэффициента диффузии ионов лития в веществе электролита/
Напряжение на аккумуляторе определяется напряжением разомкнутой цепи, поляризационным потенциалом и омическими потерями на внутреннем сопротивлении аккумулятора при протекании через него электрического тока. Ниже представлены измеренные зависимости основных параметров аккумулятора от степени его заряда.
2.2 Зависимость НРЦ от SoC при зарядке аккумулятора. Уравнение Нернста.
Нелинейный вид кривой роста напряжения в начале цикла зарядки (на рисунке 1.1) обусловлен быстрым изменением концентрации ионов лития в приэлектродной области. Напряжение разомкнутой цепи Ex определяется разностью электрохимических потенциалов катода и анода в равновесном состоянии, каждый из которых определяется уравнением Нернста:

.jpg) (1)
(1)
здесь – электрохимический потенциал катода или анода;
– электрохимический потенциал катода или анода;
R – универсальная газовая постоянная;
T – абсолютная температура;
n – число электронов, соединяемых с ионом (для лития n = 1);
F – число Фарадея;
Li+ – концентрация носителей в контактном слое электрод-электролит.
Из представленного выражения следует, что потенциал литированного электрода логарифмически зависит от степени концентрации ионов лития. Это определяет медленное изменение напряжения на аккумуляторе при изменении SoC в средней части графика зарядки. Можно показать, что при изменении концентрации в 10 раз, электродный потенциал Eх при комнатной температуре меняется примерно на 59 мВ. Типичное значение Eх для литий-железо-фосфатного аккумулятора, заряженного до 60 - 80 %, при нормальных условиях составляет 3,32 – 3, 34 В.
На рисунке 2.2 представлена экспериментально измеренная зависимость НРЦ аккумулятора от степени его заряда при комнатной температуре. Видно, что зависимость НРЦ от SoC действительно имеет логарифмический характер.
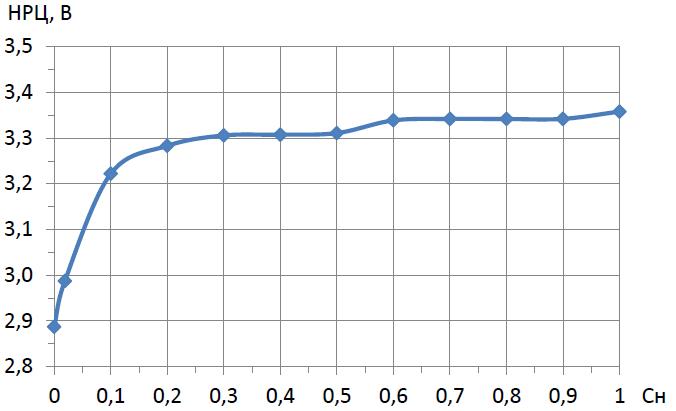

Рисунок 2.2 – Зависимость НРЦ от уровня заряда (в долях от Сн) при t = 25±3 °C
2.3 Зависимость внутреннего сопротивления от степени заряда аккумулятора
Рассмотрим эквивалентную схему, представленную на рисунке 2.1б. Как показали измерения, постоянная времени τ1=R1·C1 равна примерно 10 – 100 мсек. Величина R1 определяет величину внутреннего сопротивления Rint, которую производители аккумуляторов приводят в спецификациях на свою продукцию. Rint определяется здесь как отношение глубины провала напряжения на аккумуляторе при подаче на аккумулятор ступеньки тока (3) . При этом Rint = R0 + R1. Значение Rint определяет ток, который способен выдать аккумулятор при внешнем металлическом КЗ на его борнах. Характерное значение Rint для аккумулятора емкостью 380Ач составляет 0,3 – 0,4 мОм. Постоянная времени τ2=R2·C2 равна примерно 10 – 20 минут и определяется временем релаксации аккумулятора при снятии или подаче на него нагрузки. Постоянная времени τ2 зависит от величины протекавшего тока, и слабо зависит от степени зарядки аккумулятора.
Суммарное внутреннее сопротивление также слабо зависит от SoC. На рисунке 2.3 представлена типичная экспериментально полученная зависимость внутреннего сопротивления аккумулятора модели LT-LYP380AH от степени его заряда.
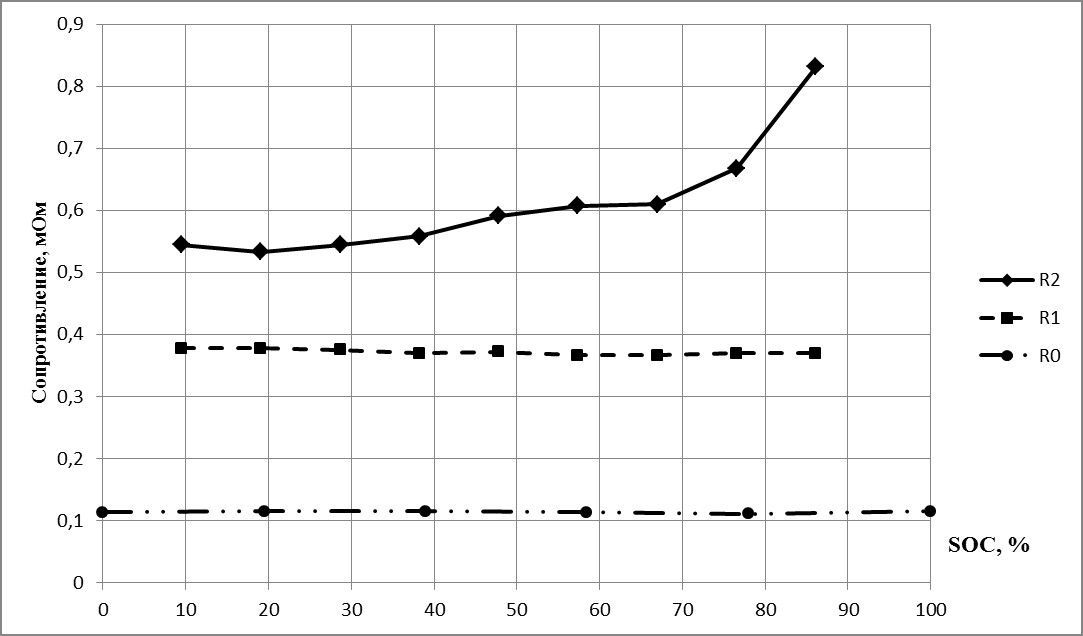

Рисунок 1.4 – Зависимость внутреннего сопротивления аккумулятора LT-LYP380AH от степени его заряда
Здесь
R0 - внутреннее сопротивление, измеренное при переменном напряжении частотой 1 кГц (при измерении использовался прибор Hioki 3554)
R1 - внутреннее сопротивление, измеренное методом 17 ГОСТ Р МЭК 896-1-95 (3) сразу после подачи ступеньки тока
R2 - внутреннее сопротивление, измеренное методом 17 ГОСТ Р МЭК 896-1-95 (3) через одну минуту после подачи ступеньки тока
Видно, что при степени заряда менее 80%, внутреннее сопротивление аккумулятора слабо зависит от степени его заряда. Рост измеренного значения R2 при приближении SoC к 100% определяется ростом поляризационного потенциала.
2.4 Поляризационный потенциал
В разных источниках поляризационный потенциал определяется по-разному. Исходя из физического смысла, поляризационный потенциал корректно определять как потенциал заряда емкости диэлектрического слоя электрод-электролит, который он имеет при зарядке/разряде малыми токами. Он определяется как отклонение измеренного напряжения на аккумуляторе от напряжения разомкнутой цепи при протекании через него тока, за вычетом падения напряжения на внутреннем сопротивлении. Физический смысл его заключается в том, что для того, чтобы начался процесс зарядки/разряда аккумулятора, конденсатор, образованный переходом электрод-диэлектрик-электролит, должен быть заряжен до определенной величины (для того, чтобы началась реакция зарядки/разряда, нужно потратить некоторое количество энергии). Поляризационный потенциал равен суммарному напряжению заряда конденсаторов на двух электродах. Величина поляризационного потенциала для свинцово-кислотного аккумулятора равна примерно 150 - 180 мВ. Эта величина определяет снижение напряжения на аккумуляторе при переходе его из режима поддерживающего заряда (при напряжении 2,23 В) в режим разряда (до напряжения 2,05 – 2,08 В).
Как было экспериментально установлено, для литий-ионного аккумулятора эта величина существенно ниже и равна примерно 3 - 5 мВ. Изменение поляризационного потенциала определялось как изменение напряжения на аккумуляторной батарее при переходе ее из режима зарядки малым током (~ 0,5 А) в режим разряда также малым током (~ 1,0 А). Тот факт, что поляризационный потенциал литий-ионного аккумулятора намного ниже, чем у свинцово-кислотного аккумулятора, по-видимому, обусловлен тем, что между литий-ионным и свинцово-кислотным аккумулятором есть принципиальное отличие. В случае свинцово-кислотного аккумулятора процесс его зарядки сопровождается протеканием химической реакции на границе электрод-электролит, связанной с преобразованием сульфата свинца в двуокись свинца и серной кислоты на одном электроде, и металлический свинец и серную кислоту – на другом. В процессе разрядки протекает обратная химическая реакция. В случае литий-ионного аккумулятора химическая реакция на границе электрод-электролит не происходит. Процесс зарядки/разряда обусловлен свободной интеркаляцией ионов лития из вещества катода в вещество анода и обратно.
Как было указано выше, при приближении SoC к 100%, происходит нелинейный рост поляризационного потенциала, обусловленный переходом к другому типу химической реакции, связанной с преобразованием вещества электролита.
2.5 Понятие 100% заряженный аккумулятор. Необходимость балансировки
Литий-ионный аккумулятор при зарядке ведет себя не так как свинцово-кислотный аккумулятор. Само понятие «аккумулятор заряжен на 100%» - у них разное. Стандарт DIN 40729 (4) определяет понятие «полный заряд свинцово-кислотного аккумулятора», как заряд с преобразованием всего активного вещества. Таким образом, свинцово-кислотный аккумулятор, заряженный на 100% - эта аккумулятор, у которой весь сульфат свинца преобразовался в металлический свинец (на отрицательном электроде) или в двуокись свинца (на положительном электроде), то есть этому понятию соответствует вполне конкретное и однозначно определяемое состояние электрохимической системы. Свинцово-кислотный аккумулятор в принципе не может быть заряжен выше 100%. Напряжение подзаряда, которое для классических обслуживаемых свинцово-кислотных аккумуляторов равно 2,23 В при комнатной температуре, примерно соответствует сумме напряжения разомкнутой цепи полностью заряженного аккумулятора и его поляризационного потенциала.
Для литий-ионного аккумулятора «степень заряда 100%» является величиной относительной. Это понятие не определяет однозначно состояние электрохимической системы. Условно за 100% заряда большинство производителей ЛИА LFP считают заряд, который аккумулятор получил при зарядке его постоянным током 0,2С до достижения напряжения 3,7 В, с последующим переходом в режим зарядки при постоянном напряжении до снижения зарядного тока до величины 0,02С. Если не остановить зарядку в этой точке, аккумулятор может заряжаться дальше. При этом, еще до достижения точки 100%, аккумулятор приближается к порогу, при котором почти все ионы лития из катода деинтеркалированы, их количество становится недостаточно для того, чтобы поддерживать химическую реакцию на прежнем уровне. В этом случае параллельно запускается другая химическая реакция, которая связанна с преобразованием вещества электролита (в котором также содержатся ионы лития), что приводит к деградации аккумулятора. Этот фазовый переход сопровождается нелинейным ростом поляризационного потенциала. Поэтому, с одной стороны, при зарядке ограничивают напряжение зарядки у литий-ионного аккумулятора, с другой стороны, в определенный момент времени искусственным образом останавливают его дальнейшую зарядку, иначе возможен так называемый перезаряд аккумулятора, то есть зарядку его до степени заряда выше 100%. Длительные перезаряд литий-ионного аккумулятора приводит к снижению его емкости, росту внутреннего сопротивления и НРЦ. Косвенным признаком того, что литий-ионный аккумулятор длительно находился в перезаряженном состоянии, является образование металлического лития в материале катода и, соответственно, увеличение НРЦ. НРЦ нормального литий-феррум-фосфатного аккумулятора, заряженного до 60 – 80 %, составляет 3,32 – 3,34 В. НРЦ литий-феррум-фосфатного аккумулятора, в катодном материале которого содержится металлический литий, может составлять 3,40 – 3,45 В.
Необходимость периодической балансировки литий-ионных аккумуляторов в батарее как раз является следствием того, что понятие «степень заряда 100%» является для ЛИА величиной относительной. Если предварительно полностью выровнять степень заряда литий-ионных аккумуляторов в батарее, с течением времени будет происходить их разбалансировка, обусловленная различием их параметров (емкость, величина саморазряда, внутреннее сопротивление), даже если батарея эксплуатируется в режиме поддерживающего заряда. Дополнительная сложность балансировки литий-железо-фосфатных аккумуляторов в батарее заключается в том, что для них характерна слабая зависимость напряжения на них от степени их заряда.
3. Математическая модель процесса зарядки ЛИАБ
Большинство производителей ЛИА, рекомендуют заряжать эти аккумуляторы методом CC/CV с переходом в режим зарядке при постоянном напряжении равном 3,7 – 3,9 В. Этот режим допустимо использовать для зарядки единичного аккумулятора, но нельзя использовать для аккумуляторной батареи, состоящей из последовательно соединенных аккумуляторов, имеющих разброс параметров. При приближении к степени заряда 100% происходит нелинейный рост напряжения на аккумуляторе, имеющем наименьшую емкость (наибольшую степень заряда), который невозможно компенсировать током балансировки. При этом процесс зарядки приходится останавливать еще до того, как все батарея будет заряжена до 100%.
Для того чтобы количественно оценить влияние разброса параметров аккумуляторов в батарее, была разработана математическая модель ее зарядки, которая позволила провести анализ на основании сравнительно простых расчетов. При этом точность полученных результатов достаточна для того, чтобы определить допустимый разброс параметров аккумуляторов в батарее и выдать рекомендации на режим ее зарядки. Влиянием температуры на процесс зарядки в данном случае мы пренебрегаем, считается, что зарядка происходит при комнатной температуре.
Для целей нашего анализа достаточно использовать упрощенную эквивалентную схему, представленную на рисунке 3.1. Предложенная схема корректна, если рассматриваются относительно медленные процессы, проходящие в аккумуляторе, постоянные времени которых составляют несколько десятков минут и более, что справедливо для типичного процесса зарядки аккумулятора в течение несколько часов.
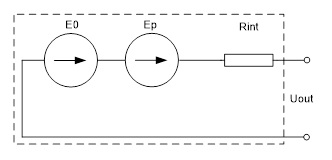

Рисунок 3.1 – упрощенная эквивалентная схема аккумулятора
При этом можно пренебречь влиянием электрической емкости С1 переходов электрод – электролит и электрической емкости С2, градиентом напряженности электрического поля в веществе электролита при протекании через него электрического тока. Также при этом можно учесть только активную часть внутреннего сопротивления Rint, величина которой принимается постоянной в процессе зарядки, так как, как было показано выше, внутреннее сопротивление слабо зависит от степени заряда. При этом необходимо правильно учесть влияние поляризационного потенциала.
3.1 Математическая модель единичного аккумулятора
На основании рассмотрения модели, представленной на рисунке 3.1, можно проанализировать влияние разброса параметров аккумуляторов на разброс напряжения на них в процессе зарядки и на величину конечной степени заряда, до которой может быть заряжена аккумуляторная батарея. На рисунке 3.2 представлен усредненный и сглаженный профиль зарядки аккумулятора модели LT-LYP380 постоянным током зарядки равным 0,2С до достижения напряжения на аккумуляторе 3,7 В, с переходом в режим зарядки при постоянном напряжении 3,7 В до снижения тока до величины 0,02 С. Для аккумулятора емкостью 380 Ач ток 0,2С будет равен 76 А. При зарядке другими токами профиль зарядки качественно будет иметь такой же характер, но величина падения напряжения будет отличаться на величину падения напряжения на внутреннем сопротивлении аккумулятора.
При любом токе напряжение на аккумуляторе определяется следующим выражением:
Uout=E0(SoC)+ Ep(SoC,I)+R_int (SoC)·I(SoC) (5)
Рассмотрим функции δUout = f(δC), δUout = f(δRint), δUout = f(δQ0). Здесь δUout – отклонение напряжения на аккумуляторе как функция некоторой переменной. δC, δRint, δQ0 – соответственно отклонение номинальной емкости, внутреннего сопротивления и начального заряда аккумуляторов от некоторой равновесной величины. Определяя значение конкретных функций можно определить влияние разброса конкретных параметров на разброс напряжения и на процесс зарядки аккумулятора.
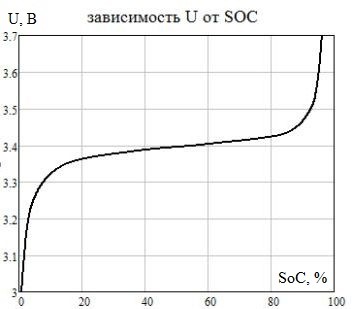

Рисунок 3.2 – Сглаженный профиль зарядки аккумулятора током 0,2С с переходом в зарядку стабилизированным напряжением 3,7 В
3.2 Влияние разброса значений внутреннего сопротивления
Рассмотрим батарею, состоящую из аккумуляторов с одинаковой емкостью 380 Ач и разными внутренними сопротивлениями Rint = R0int + δ Rint. Пусть, например, Rint1 = 1,0 мОм, Rint2 = 1,2 мОм (20%). Как показали измерения, внутреннее сопротивление аккумулятора сравнительно слабо зависит от степени его заряда. Поэтому, из (5) можно получить следующее выражение:
δUout(δR_int)=∂Uout/∂Rint·δR_int=I·δR_int (6)
Пусть, например, ток зарядки равен 76 А (0,2Сн). Очевидно, что разница в напряжениях двух аккумуляторов будет равна δUout = δRint·I(SoC) = 16 мВ в течение всего цикла зарядки и спадает к нулю к концу зарядки аккумулятора. При этом разброс сопротивлений не приводит к снижению максимально допустимого заряда батареи. Данный пример проиллюстрирован на рисунке 3.3.
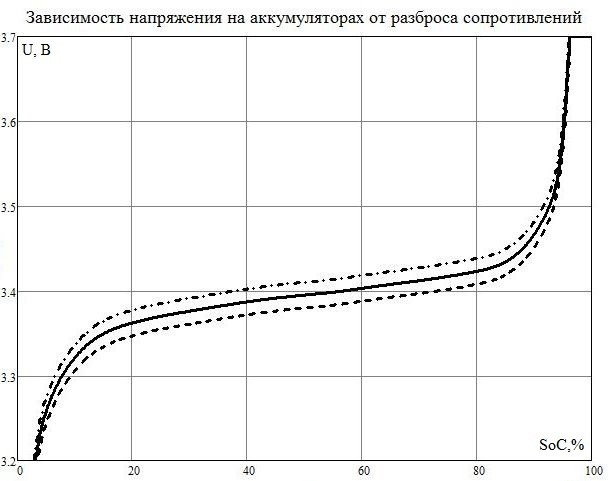

Рисунок 3.3 – Зависимость напряжения на аккумуляторах от разброса сопротивлений
3.3 Влияние разброса емкости
Рассмотрим график изменения напряжения на аккумуляторе от степени его заряда, представленный на рисунке 3.1. Рассмотрим отклонение напряжения на аккумуляторах батареи в процессе ее зарядки как функцию отклонения их емкостей от равновесной величины δUout = f(δC).
δUout(δС)=∂Uout/∂С·δС (7)
Согласно определению, C=Q_max – максимальный заряд, до которого может быть заряжен аккумулятор. С другой стороны, степень заряда аккумулятора SOC=Q/Q_max. Поскольку аккумуляторы в батарее соединены последовательно, при зарядке они получают один и тот же заряд Q. Таким образом,
δC≈-δSoC – при приближении SOC к 100%. Таким образом, формулу (7) можно переписать в следующем виде:
δUout(δSoC)≈-∂Uout/∂SoС·δSoC (8)
Для анализа зависимости разброса напряжения от разброса емкости допустимо анализировать разброс напряжения от степени его заряда. Рассмотрим функцию заряда «при нулевом токе зарядки»:
U0(SoC)=U(SoC)-R_in·I(SoC) (9)
Здесь U(SoC) - функция заряда аккумулятора током 0,2С, график которой представлен на рисунке 3.2. Функция U0(SoC) формально определяет падение напряжения на аккумуляторе при «зарядке» его нулевым током до степени заряда 100%. При этом предполагается, что значение U0 сверху не ограничено. Анализ поведения функции U0 и позволит определить разброс напряжений аккумуляторов, имеющих разную степень заряда в батарее. Поскольку в линейной части графика зарядки поляризационный потенциал практически не зависит от S0C, то его влияние в линейной части графика учитывается как добавочная величина внутреннего сопротивления. В нелинейной части именно поляризационный потенциал определяет поведение функции U0(SoC).
Для простоты анализа рассмотрим аккумуляторную батарею, состоящую из трех аккумуляторов. Пусть емкость первого аккумулятора равна C0, второго – C0 - δC, третьего - C0 + δC. Таким образом, в процессе зарядки степень заряда второго аккумулятора будет все время больше чем у первого аккумулятора на величину δSoC ≈ δC, третьего – меньше на ту же величину δC. Для определенности рассмотрим профиль зарядки, представленный на рисунке 3.2. Заряд начинается из состояния SoC = 0% постоянным током 0,2С до достижения среднего напряжения на аккумуляторах Uav = 3,70 В (суммарно 11,10 В на батарею). После этого происходит переход в режим зарядки при среднем напряжении на аккумуляторе 3,70 В со снижением тока до 0,02С.
Для анализа используем функцию зарядки U0(SoC). Среднее значение напряжения на аккумуляторах определено зарядным устройством и равно Uav. Отклонение напряжения на аккумуляторе δUi от среднего значения определяется разбросом степени заряда δSoCi. Это проиллюстрировано на рисунке 3.4.
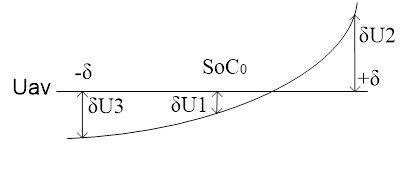
Рисунок 3.4 – Пример, поясняющий принцип определения разброса напряжений на аккумуляторах
Для каждого конкретного значения SoC0 справедливы выражения:
δU2 - δU1= U0(SoC0+δ) - U0(SoC0) (10)
δU1 - δU3 = U0(SoC0) - U0(SoC0-δ) (11)
С учетом того, что ∑iδUi = 0 мы имеем систему из трех линейных уравнений с тремя неизвестными. Решая ее, мы находим значения напряжений для каждого аккумулятора:
U1 = Uav + δU1 (12)
U2 = Uav + δU2
U2 = Uav + δU2
При этом нужно учесть физические ограничения, связанные с тем, что напряжение на отдельном аккумуляторе не может быть ниже величины Umin:
Umin = E0(SoC) + Rin (SoC) · I(SoC) (13)
так как невыполнение этого условия означало бы изменение знака поляризационного потенциала и прекращение процесса зарядки аккумулятора.
На рисунке 3.5 представлен график зарядки батареи током 0,2С до достижения среднего напряжения на аккумуляторе 3,70 с переходом в режим зарядки при этом напряжении. Разброс емкости равен + 2,5%. При достижении степени заряда 94% напряжение на аккумуляторе 3 становится выше 3,70 В, и в этот момент зарядка должна быть остановлена. Излом кривых 1 и 3 объясняется том, что кривая напряжения аккумулятора 2 растет очень быстро (как гиперболическая функция). При расчете батареи, состоящей из большего числа частиц, этот излом сглаживается. Таким образом, видно, что при среднем значении напряжения на аккумуляторе, равном 3,70 В максимальная степень заряда, до которого может быть заряжена батарея, составляет 94%.

Рисунок 3.5 – График зависимости разброса напряжений на аккумуляторах от разброса SoC при зарядке до среднего напряжения 3,7 В. 1 – δC = 0 %, 2 - δ = +2,5 %, 2 - δ = -2,5 %
4. Рекомендации по режиму зарядки
Как было показано, в случае зарядки аккумуляторной батареи, состоящей из многих аккумуляторов, имеющих разброс параметров, ее практически невозможно заряжать до достижения среднего напряжения на аккумуляторе 3,70 В, как это рекомендуются для единичного аккумулятора. Ситуацию может улучшить применение специализированных методов зарядки, основанных на организации обратной связи между системой управления батареей и зарядным устройством, предполагающих снижение тока зарядки батареи до величины тока балансировки, но это приводит к существенному увеличению времени зарядки. Для улучшения ситуации можно попытаться уменьшать среднюю величину напряжения зарядки отдельного аккумулятора в батарее.
4.1 Степень заряда, достигаемая при различных уровнях напряжения стабилизации
Величина напряжения перехода из режима CC в режим CV влияет на величину степени зарядки, до которой заряжается аккумулятор при снижении тока его зарядки до величины 0,02С.
На рисунке 4.1а представлена зависимость напряжения от времени зарядки при различном значении напряжения перехода в режим CV. На рисунке 4.1б - зависимость тока от времени зарядки.
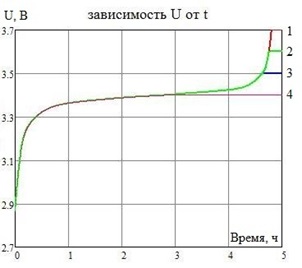
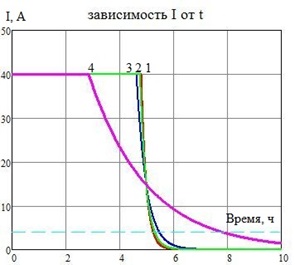
Рисунок 4.1
а - зависимость напряжения от времени зарядки б - зависимость тока от времени зарядки
На графиках напряжение перехода в режим CU равно: 1 – 3,70 В, 2 – 3,60 В, 3 – 3,50 В, 4 – 3,40 В. На рисунке 4.2а представлена зависимость времени зарядки аккумулятора до снижения тока его зарядки до 0,02С от величины напряжения перехода в режим CV. На рисунке 4.2б - зависимость тока от времени зарядки. Видно, что при изменении величины напряжения перехода в режим CVот 3,7В до 3,45В, время зарядки аккумулятора и степень, до которой он заряжается почти не изменяется.
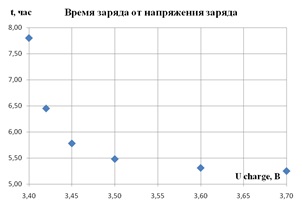
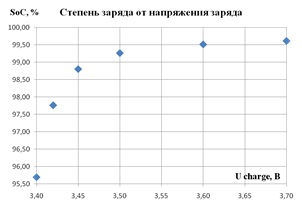
Рисунок 4.2
а – зависимость напряжения от времени зарядки б – зависимость тока от времени зарядки
Таким образом видно, что батарею, так же как и отдельный аккумулятор можно заряжать до меньшего напряжения, например, до 3,40 – 3,45 В с последующим переходом в режим зарядки стабилизированным напряжением.К недостаткам данного метода можно отнести то, что время зарядки единичного аккумулятора при этом несколько увеличивается. На рисунке 4.3а представлен график зарядки батареи током 0,2С до достижения среднего напряжения на аккумуляторе 3,40 с переходом в режим зарядки при этом напряжении. Разброс емкости равен + 2,5%. Зарядка остановлена при снижении тока до 0,02С, при этом степень заряда аккумуляторной батареи составила 96%. На рисунке 4.3б представлен тот же график во временном масштабе.
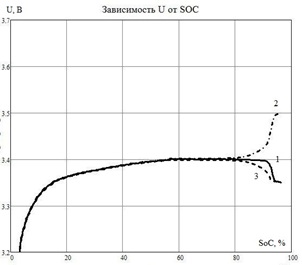
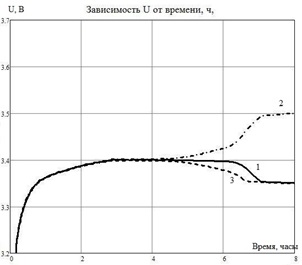
Рисунок 4.3– График зависимости разброса напряжений на аккумуляторах 1 – δC = 0 %, 2 - δС = +2,5 %, 3 - δС = -2,5 %
а - от степени заряда б - от времени зарядки
ЗаключениеТаким образом, видно, что при зарядке аккумуляторной батареи, состоящей из многих последовательно соединенных литий-железо-фосфатных аккумуляторов, полезно снизить среднее напряжение зарядки аккумулятора до 3,40 – 3,45 В. Точное значение среднего напряжения зарядки нужно определять для конкретного типа аккумулятора.
Заключение
- В работе рассмотрена модель литий-железо-фосфатного аккумулятора как активного двухполюсника, параметры которого (напряжение генератора и внутреннее сопротивление) нелинейно зависят от тока зарядки/разряда, степени заряда и температуры. Для определения параметров модели использовались экспериментальные данные.
- В рамках выполненной работы рассмотрена эквивалентная схема аккумулятора, наиболее адекватно описывающая поведение аккумулятора при зарядке. Рассмотрены зависимости основных параметров аккумулятора от степени его заряда, приведены экспериментально полученные данные.
- На основании этого рассмотрена простая модель ЛИА, которая позволила проанализировать поведение литий-ионной батареи при ее зарядке, и влияние разброса параметров отдельных аккумуляторов на процесс зарядки.
- На основании расчетов получены рекомендации на параметры напряжения зарядки литий-железо-фосфатной аккумуляторной батареи. Показано, что величина среднего напряжения, приложенного к аккумулятору при зарядке батареи, должна быть снижена до до 3,40 – 3,45 В. Конкретная величина должна определяться исходя из зависимости НРЦ от степени заряда для конкретного типа аккумуляторов.
- На основании расчетов было рекомендовано собирать аккумуляторную батарею из аккумуляторов, имеющих разброс по емкостям не более + 2,5%, по внутреннему сопротивления – не более + 20%.
Список литературы
- M. Chen, G.A. Rincon-Mora, Accurate Electrical Battery Model Capable of Predicting Runtime and I-V performance, IEEE Transaction on energy conversion, v. 21, no. 2, June 2006.
- OHMIC MEASUREMENTS: THE HISTORY AND THE FACTS. Glenn Albér, PresidentAlbércorp, Boca Raton, FL. http://www.alber.com/Docs/Brochure_WhitePaperG_Alber.pdf
- ГОСТ Р МЭК 896-1-95 «Свинцово-кислотные стационарные батареи. Общие требования и методы испытания. Часть 1. Открытые типы».
- СтандартDIN 40729 Akkumulatoren – “Galvanische Sekundärelemente – Grundbegriffe”, 1985